DKVS: Distributed Key-Value Store --- general description

Outline of this document

1. Project background
2. General description
3. Project goals

Context

The aim of this project is to develop a large program in C on a "system" theme. This year framework concerns "peer-to-peer" networks. More precisely, you'll have to implement a key-value associations system (hashing system) distributed over a network: a "(distributed) key-value store" (DKVS) or "distributed hash table (DHT)". You'll have to develop, following a step-by-step specification, a simplified version of such a system, inspired from Amazon's Dynamo (you don't have to read that paper; it's just for reference, if you're interested).
All the basic concepts required for this project are introduced here in a simple way, assuming only standard "user" knowledge of a computer system. If you have any doubts about terminology, the glossary at the end of the document may come in handy.

Global description

Minimal API

A DKVS or DHT can be seen as a version of Java's Map that would be made robust by its redundant distribution across multiple computers (instead of remaining locally in the memory of a single one). Such a system offers, of course, a simple user interface, very similar to an associative table (like Map in Java), but behind distributes the actual data storage over several servers. On the one hand, this increases data availability, since several machines have copies of the data (in case one or other machine is unavailable), and on the other, it increases total storage capacity (by adding up the capacities of all the machines involved).

The minimum user interface (API) can be summarized as follows:

put(key, value, N, W);
value = get(key, N, R);

The put() operation adds (or updates) data to the system by associating the value value with the key key. Such a key can then be used to retrieve the associated value by means of a get() operation. These operations are executed by a "client" machine, which sends the corresponding requests to "server" machines and coordinates their responses (details below). Additional parameters (N, W, and R, explained in more detail below) allow to configure the desired level of redundancy and balance it against the expected level of performance (robustness, access time):

• N indicates how many servers should, in principle, store the value (i.e. the maximum number of servers to contact);
• W (like "write") and R (like "read") determine the minimum number of servers that should respond positively to a put() and get() operation respectively.

An appropriate choice of these values enables the global system to withstand certain server or network failures, while still allowing reasonable time performance for put() and get() operations.

At the global level, in response to a put() or get() command, the "client" machine will contact between W or R and N "server" machines and, depending on their response (we'll explain how in detail later), will itself respond with a failure or success (consistent responses; we'll say that the quorum W or R has been reached).

Examples

Let's look at a few examples (where the association between the value b and the key a is noted in a compact way as a:b):

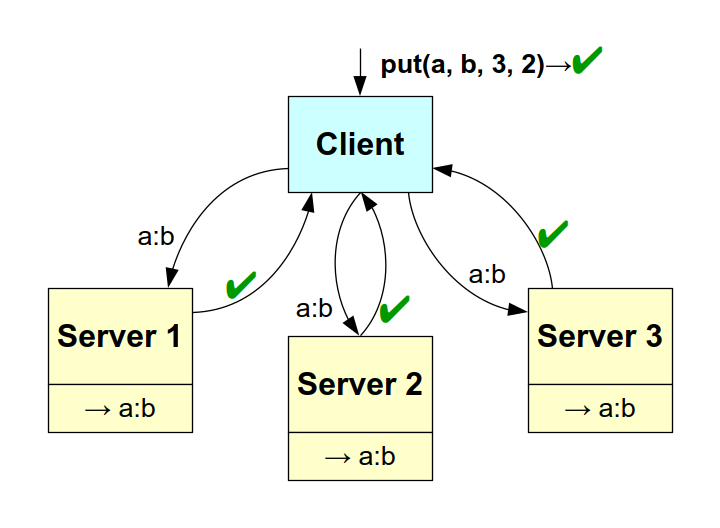
Figure: example of a successful put() operation.

In the example illustrated above, the client executes a put() operation requested for N=3 servers, with a minimum of W=2 (simple quorum) in agreement. In the case illustrated, all 3 servers receive the request, store the a:b association and respond positively; so the client responds with a success.

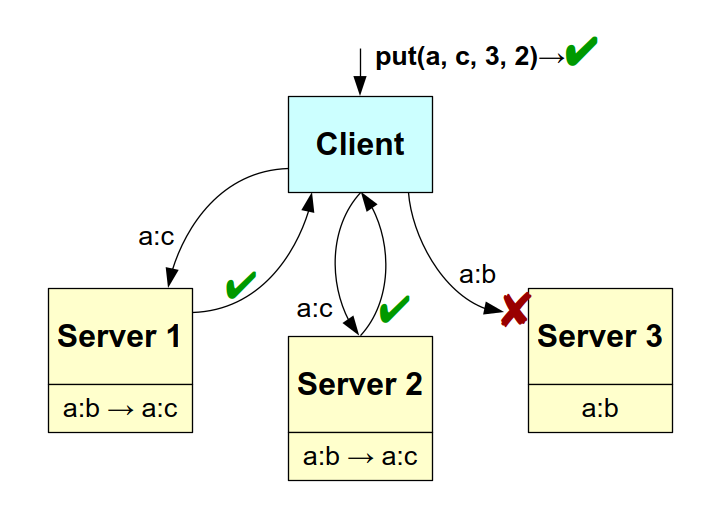
Figure: example of put() operation with network failure.

Suppose now (image above) that the client performs a new put() operation to update the previous value (replace b with c). But this time the message sent to "Server 3" is lost. The first two servers update their own association and store a:c, then respond positively; but "Server 3", being unaware of this, does nothing at all (keeps the a:b association and responds to nothing at all). At client level, however, the operation is a success, since the quorum of W=2 servers responding positively has been reached.

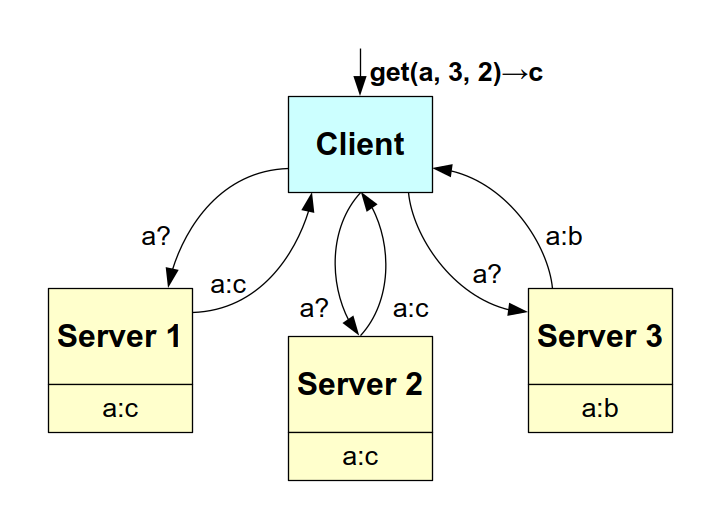
Figure: example of a successful get() operation.

Let's continue the example by now imagining that the client executes a get() operation to retrieve the value associated with the key a; and let's suppose that all the N=3 servers receive the request and respond. However, as it stands, they don't answer the same thing: one answers b and two answer c. At the client level, however, it's a success and the value c is returned, since it has reached the quorum of R=2 (the case where several different values reach the quorum will be dealt with in the corresponding detailed handout).

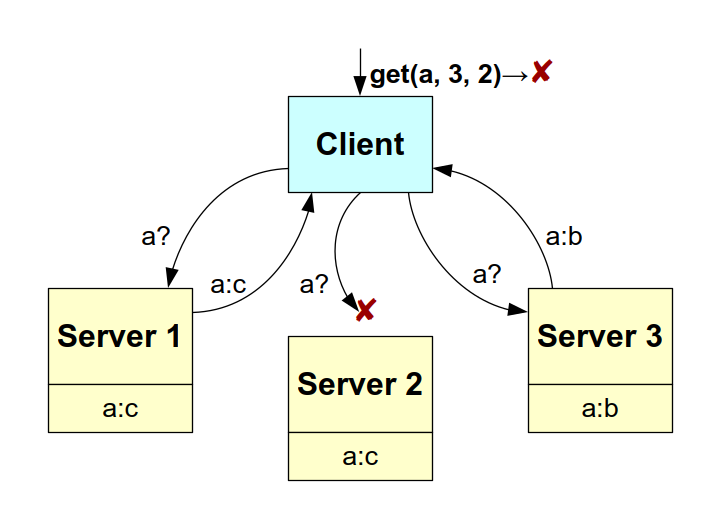
Figure: example of a failed get() operation.

To conclude this example, let's suppose that the client again executes a get() operation for key a, but that "Server 2" is unreachable. The client receives only two values: b and c, neither of which reaches quorum R=2. The client therefore responds with a failure. The parameters N=3, W=R=2 were chosen to withstand one error; but here we now have two (a write on "Server 3" and a read on "Server 2"), hence the failure.

Partial distribution -- (1) Key ring

The previous example illustrates a simple scenario in which all servers store all data. This is not realistic in practice for large data sets stored on a large number of servers. In reality, the space of possible keys is partitioned into different segments, each assigned to a server (a single server can be assigned to several segments; see the notion of "node" below). The idea is to order the space of possible keys in ascending order (this is called the "key ring" or "ring"; see illustration below), so that servers can be assigned to it, each responsible for the slice of keys up to their own node projection(s) (which are also values, in the same value-space as the keys). In this project, we'll be using the SHA-1 algorithm to represent/project the keys and the nodes in the key ring.

Let's give an example: suppose for simplification that we map the keys to an integer between 0 and 255 and let's suppose we project 5 servers (A to E) as follows:

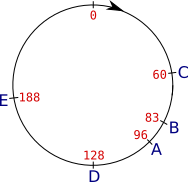
Figure: example of 5 servers in the key ring.

In reality, the SHA-1 values we're going to use to project the keys and the nodes vary between 0 and 1461501637330902918203684832716283019655932542975, which isn't easy to represent graphically...

To determine which server(s) to contact for a given key, the client calculates the key's SHA-1 code (32 in this example, shown in green) and then searches in ascending order for the first matching server, i.e. the first server SHA-1 code (60 in this example):

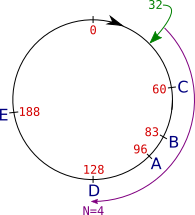
Figure: example of key projection in the key ring.

He then continues in ascending order until he has found N matching servers.

Partial distribution -- (2) Nodes

So far, we haven't overemphasized the difference between nodes and servers, since each of the six nodes in the previous example corresponds to a different server. But if we simply spread different servers across the key ring, this can harm the efficiency of the system in practice; typically, when a server fails, it leaves a large "hole" in the key ring. For this reason, it's preferable for the same server to be distributed over different parts of the key ring. Hence the notion of "node": a single server (real machine) corresponds to several nodes (abstraction) in the ring. The same server continues to manage all its keys (and values) but can, thanks to the notion of "node", appear at several places in the key ring. A key ring node is therefore a pure abstraction, representing simply one of the possible projections of a server in the key ring.

To illustrate this, let's consider that in the previous example, the letters (A-E) indeed correspond to the servers, and let's add an index to represent the nodes. For example, let's decide to have 9 nodes:

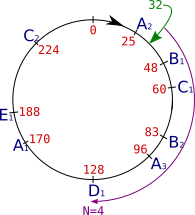
Figure: example position ring with 5 servers in 9 nodes.

Note: the position of the nodes/servers in the ring can be quite arbitrary.
[end of note]

From the point of view of explaining how the client works, this changes almost nothing to what has been described above; simply, it's now possible that, for the same request, the client may actually contact the same server several times: in this case, we do not count this server several times: when searching for N servers, we therefore don't count the nodes coming from a server of a node already visited (in other words: we count the number of different servers responding to the request and not the number of nodes). This is why, in the above illustration, the search N=4 covers 5 nodes: node B2 is not counted, as it corresponds to a server (B) already contacted (via B1).

To simplify for this project, we'll assume that the client knows the list of nodes and servers in advance (this will be a configuration file), rather than discovering them via another network protocol.

A more complete example is detailed below.

Project goals and organization

During the 8 weeks of this project, you will gradually implement, piece by piece, the three key components of a distributed hashing system:

• all the local work on a server (key-value storage, query responses);
• the put() operation on the client side;
• the get() operation on the client side.

You'll also need to develop useful additional tools to observe and analyze the behavior of the DKVS. All these tools will be developed as independent programs (set of tools on the usual command line).

Finally, in the last week, you will also carry out an experimental study of the impact of different parameters on system performance.

To help you get organized, please also consult the project foreword page (and read it entirely).

Data structures (general description)

Here is a general description of the main data structures required for this project. Details of their implementation will be given later, when necessary, in the corresponding specific handout.

• dksv_key_t: to represent keys; typically a string;
• dksv_value_t: to represent values; typically a string;
• bucket_t: internal element ("bucket") of a local hash table (on servers);
• client_t: representation of a client;
• Htable_t: to store locally (on each server) the key-value associations for which it is responsible;
• node_t: representation of a server (actually: a node, but the distinction won't be introduced until step 6);
• ring_t: key ring: association table between positions in the ring and servers represented as a list of nodes (node_t).

Another example

Here is a complete example of the final version of this project. During the semester, there will be various simplified versions of this model: we'll gradually move from a very simple version to the example given here.

Let's suppose we want to store string-to-string associations in a network of S=5 servers, to perform, for example, operations such as get("my_key") or put("my_key", "my_value").

Suppose also that (see figure below):

• the Hring() function for hashing keys at global level (position ring) returns values between 0 and 255;
• the Hlocal() function for hashing keys at local level (each server) returns values between 0 and 42;
• M = 9 (a total of 9 nodes in the position ring);
• N = 4 (read/write operations on 4 servers);
• R = 2 (2 valid reads are required to retrieve a value from the network);
• W = 3 (3 valid writes are required to insert a value into the network);
• the distribution of servers and nodes in the position ring is as follows:
  • server A: 25, 96, 170;
  • server B: 48, 83;
  • server C: 60, 224;
  • server D: 128;
  • server E: 188.

Here is a figure illustrating this architecture:

Figure: a DKVS example with S=5, N=4, W=3 and R=2.

Furthermore, suppose that:

• server B is down (it will be detected as down via a timeout);
• Hring("my_key") = 32;
• and Hlocal("my_key") = 10.

What happens with a put("my_key", "my_value")?

1. We calculate Hring("my_key"), which gives 32.
2. We try to write to N different servers in the ring, starting from 32: this gives servers B, C, A and D;
   node 83 (server B) is ignored, as it corresponds to a server already under consideration (B).
3. Since B has fallen, only writings to C, A and D do work.
4. Since W=3 and 3 servers have responded positively to the write, the write is considered successful.

In addition, on each of the servers A, C and D, the writing of the value "my_value" associated with the key "my_key" is done locally. With the choice we've made for local implementation, this is done using a (local) hash table whose hash function is Hlocal().

We therefore calculate Hlocal("my_key"), which is 10, and store the pair ("my_key", "my_value") at position 10 of the local array.

What happens next when you get("my_key") (while B is still down)?

1. We calculate Hring("my_key"), which gives 32.
2. We try to read positions from 32 on N different servers in the ring: this gives servers B, C, A and D.
3. As B has fallen, only C, A and D respond, each with "my_value".
4. Since we have more than R=2 matching answers, we return "my_value".

What happens with get("my_key") if B is operational but C has fallen?

Steps 1 and 2 proceed in the same way, but in step 3, B answers "anything" (either unknown, or an old value, let's assume different) and A and D each still answer "my_value". We therefore always have at least R=2 coherent answers, so we return "my_value".

What if A or D fall too?

In this case, the value "my_value" will be read only once, and "anything" will be read once. No value has been read at least R times, so the global read is a failure.

Glossary

• bucket: a hash table element;

• client: the computer from where the distributed key-value store manipulation instructions are given;

• hash function: the function that associates a key with an index to access a value stored in the hash table;
  Example: H() in index = H("my_key"); we will actually have two different hash functions in this project:

  • the position ring function, which transforms a key (or a node) into a ring position (integer, type size_t);
  • the local hash function, local to each server, to store the values in its hash table;

• hash table elements: sometimes called "buckets", the actual implementation of the content of a hash table;

• index: position in a hash table local to a server; result of key hashing by the local hash function;
  Example: index = Hlocal("my_key");

• key: unique identifier for a value to be stored; typically a string;
  Example: "my_key" in get("my_key") or in put("my_key", "my_value");

• M: total number of nodes in the key ring; we must have M ≥ N;

• N: maximum number of servers storing a particular key; also the maximum number of reads/writes performed for a given value (see R and W);

• node: abstraction (= conceptual entity) of the key ring covering a subset of possible positions; this is an abstraction because a real server may represent several nodes (this node/server distinction allows the same server to be distributed to several different non-consecutive locations in the position ring);
  Example: server 23 covers (= is represented by) nodes 3, 11 and 17;

• position: position in the ring; result of hashing the key with the ring-specific hash function;
  Example: position = Hring("my_key");

• R: (as in "read") number of functional servers required to retrieve a value from the network; a read operation attempts to read from N servers and succeeds if (at least) R of these reads are successful and coincide;

• ring, position ring: abstraction used to map keys to servers (represented by nodes positioned on the ring); this is the same set of values as for keys (key ring and position ring are the same thing viewed differently: from the key or from the node perspective);

• S: (as in "server") number of servers in the network; we must have M ≥ S ≥ N;

• server: machine in the network used to physically store data; represented by one or more nodes in the position ring;

• value: a value to be stored in the distributed hash table; typically a string;
  Example: "my_value" in put("my_key", "my_value");

• W: (as in "write") number of functional servers required to store a value in the network; this is the minimum number of replications of each value in the network; a write operation attempts to write to N servers and succeeds if (at least) W of these writes are successful.